



相当算は、小学生5年生で習う割合を使って問題を解きます。
相当算を解くためのポイント
・割合を理解していること
・問題を正確に数直線に書くこと
以下の3パターンの基本例題をマスターしましょう。
<①相当算1>
【問題】
Aさんは150円の飲み物を買うために、持っていたお金の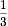 を使いました。
最初に持っていたお金はいくらあったでしょう。
を使いました。
最初に持っていたお金はいくらあったでしょう。
【解法】
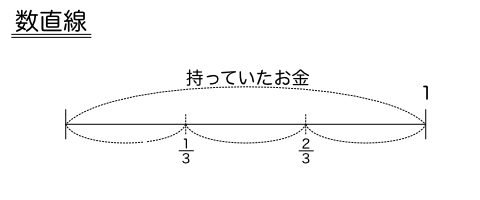
今回の問題で割合の「もとになる数」は「持っていたお金」となるため、「持っていたお金」が数直線全体の値となります。
つぎに、Aさんは「持っていたお金」の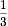 を使って飲み物を買ったため、数直線を3等分します。
を使って飲み物を買ったため、数直線を3等分します。
3等分した1個分が飲み物の代金(150円)となるため、最初に「持っていたお金」は
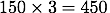 (答え:450円)
(答え:450円)
となります。
<②相当算2>
【問題】
Aさんはある本を読んでいました。1日目は全体の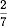 読み進め、2日目は残りの
読み進め、2日目は残りの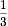 読み進め、
3日目は残りの
読み進め、
3日目は残りの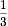 読み進めたところ、あと20ページ残っています。この本の全体のページ数は何ページでしょう。
読み進めたところ、あと20ページ残っています。この本の全体のページ数は何ページでしょう。
【解法】
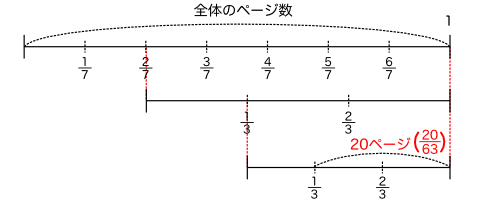
今回の問題で割合の「もとになる数」は「本全体のページ数」となるため、「本全体のページ数」が数直線全体の値となります。
「本全体のページ数」を1としたとき、3日目に残っているページ数の割合は1日目、2日目、3日目の残っているページ数の割合を掛け算すれば求まります。
つまり、
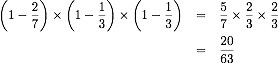
です。
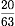 が残りのページの割合となるため全体のページ(もとになる数)は
が残りのページの割合となるため全体のページ(もとになる数)は
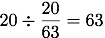 (答え:63ページ)
(答え:63ページ)
で求まります。
<③相当算3>
【問題】
Aさんと兄と弟はお母さんからアメ玉をもらいました。
Aさんは全体の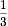 をもらい
兄は全体の
をもらい
兄は全体の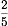 をもらい
弟は全体の
をもらい
弟は全体の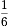 をもらいました。
まだ飴玉が30個残っていたので10個ずつわけました。
をもらいました。
まだ飴玉が30個残っていたので10個ずつわけました。
お母さんが配ったあめ玉は何個でしょうか。
【解法】
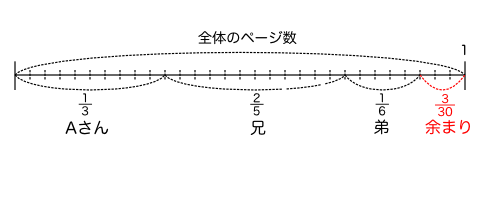
今回の問題で割合の「もとになる数」は「お母さんが配ったアメ玉」となるため、「お母さんが配ったアメ玉」が数直線全体の値となります。
また、Aさんと兄と弟の割合を通分すると、
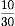 、
、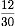 、
、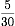 になります。
になります。
3人分の割合を足し合わせると
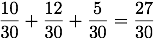
となります。
全体の1から3人の割合(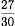 )を引くと
)を引くと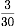 になり、
その値が余ったアメ玉(30個)の割合となります。
になり、
その値が余ったアメ玉(30個)の割合となります。
よって、「お母さんが配ったアメ玉」は
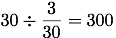 (答え:300個)
(答え:300個)
となります。