



2014年10月 7日(火)
本日は、インターネット上で2桁×2桁を図を使って説明している記事を見つけましたので、ご紹介させて頂きます。
--->>> 2ケタ同士のかけ算があっという間にできてしまう恐るべき方法
私としては、ひっさんで計算してほしいのでオススメしませんが、皆様の理解に繋がればと思いご紹介させて頂きます。
2桁の計算なので、例えば、12×21という計算を行ってみましょう。
(答えは252です。)

まずは、図1のように正方形を傾けた図を想像してください。
左斜め上には、かけ算の左側の10の位の値分、線を引きます。(今回の例だと1本)
右斜め下には、かけ算の左側の1の位の値分、分線を引きます。(今回の例だと2本)
左斜め下には、かけ算の右側の10の位の値分、線を引きます。(今回の例だと2本)
右斜め上には、かけ算の右側の1の位の値分、分線を引きます。(今回の例だと1本)
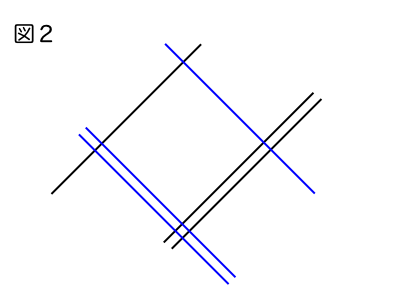
引いた結果が図2のようになります。

図3の通り辺と辺が交差した点の個数を数え、○で囲んだ点の個数を合計してください。
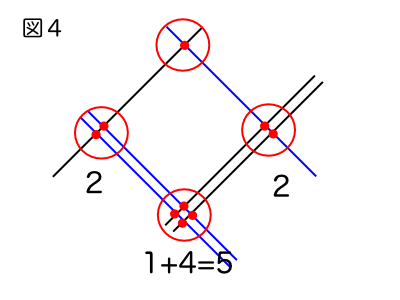
結果は図4の通りとなり左から100の位、10の位、1の位とすると、252になります。
次に繰り上がりがある計算を考えましょう。
例えば、24×23という計算を行ってみましょう。(答えは552)
やり方は全て先ほどの方法と同じです。
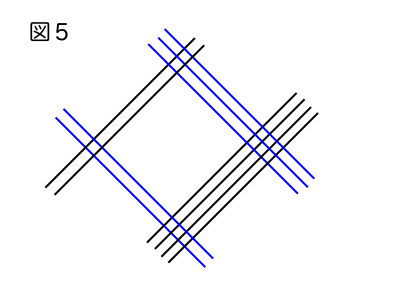
線を引いた結果が図5の通りとなります。
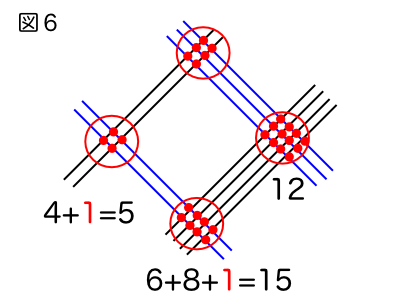
点の数を数えた結果が図6の通りとなります。ただし、点の数え方に注意があり、繰り上がりがある場合は次の位に繰り上がった分の数だけ足して上げる必要があります。
(繰り上がった数は赤字で示しています。)
結果は552となります。
みなさん、色々なやり方を考えるので教える際の参考になります。
また、色々な情報をホームページを通じて報告したいと思います。